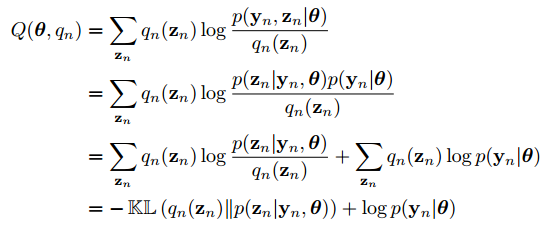Bound Optimization - Expectation Maximization

Trong bài viết này chúng ta sẽ đề cập đến một lớp các thuật toán được gọi là Bound Optimization hoặc MM Optimization. Trong ngữ cảnh minimization, MM được hiểu là Majorize-Minimize, trong ngữ cảnh maximization, MM được hiểu là Majorize-Maximize. Chúng ta sẽ nói về một trường hợp đặc biệt của MM là Expectation Maximization hoặc EM.
I. Định nghĩa
Giả sử mục tiệu là maximize hàm $L(\theta)$ , chẳng hạn như hàm log likelihood với tham số $\theta$ . Cách tiếp cận cơ bản trong MM là đi xây dựng surrogate function $Q(\theta, \theta^t)$ là một chặn dưới của $L(\theta)$ , $Q(\theta, \theta^t) \le L(\theta)$ và $Q(\theta^t, \theta^t) = L(\theta^t)$ . Nếu các điều kiện này thỏa mãn, ta gọi minorizes .
Sau đó thực hiện cập nhật sau mỗi bước:
$\theta^{t+1}= \operatorname*{argmax}_\theta Q(\theta, \theta^t)$
Điều này đảm bảo sự đơn điệu tăng trong hàm mục tiêu ban đầu.
$l(\theta^{t+1}) \ge Q(\theta^{t+1}, \theta^t) \ge Q(\theta^t, \theta^t) = l(\theta^t)$

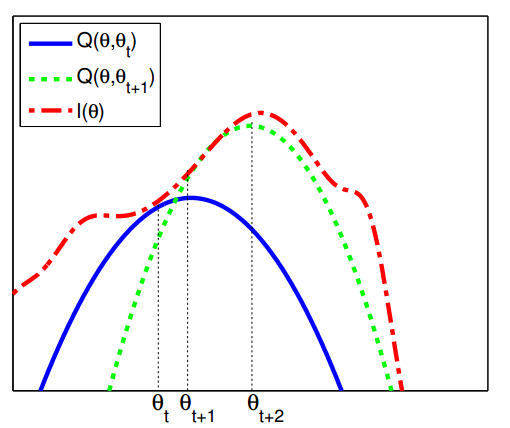
Minh họa Bound Optimization: Đường nét đứt màu đỏ là hàm mục tiêu gốc, đường nét liền màu xanh là lower bound tại vị trí $\theta^t$ , nó tiếp xúc với hàm objective gốc tại vị trí $\theta^t$ , và maximum của đường này là $\theta^{t+1}$ . Đường nét đứt màu xanh tiếp xúc với hàm mục tiêu gốc tại $\theta^{t+1}$ , maximum mới là $\theta^{t+2}$ .

II. Thuật toán Expectation Maximization (EM)

EM là thuật toán để tính MLE (Maximum Likelihood Estimation) hoặc MAP parameter estimate cho probability models mà có dữ liệu không đầy đủ (missing data) hoặc có biến ẩn (hidden variables).
“A general technique for finding maximum likelihood estimators in latent variable models is the expectation-maximization (EM) algorithm.”
Page 424, Pattern Recognition and Machine Learning, 2006.
“… if we have missing data and/or latent variables, then computing the [maximum likelihood] estimate becomes hard.”
Page 349, Machine Learning: A Probabilistic Perspective, 2012
EM gồm 2 bước chính:
1. E step (Expectation step): Estimate the missing variables in the dataset.
2. M step (Maximization step): Maximize the parameters of the model in the presence of the data.
Một số ứng dụng của EM như fit mixture models (such as Gaussian mixture model), fit a multivariate Gaussian (khi missing data), fit robust linear regression models,…

1. Lower bound

Mục tiêu của thuật toán EM là maximize log likelihood của dữ liệu quan sát được (observed data):

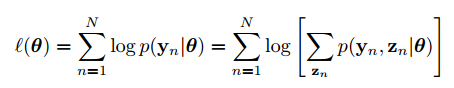
trong đó là dữ liệu quan sát được (visible variables) còn là dũ liệu ẩn (visible variables).
Xét một tập hợp các phân phối tùy ý (arbitrary distributions) đối với mỗi biến ẩn , hàm log likelihood có thể viết lại như sau:

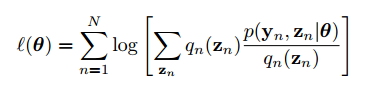
Nhắc lại bất đẳng thức Jensen (Jensen’s inequality): Với hàm lồi (convex function) , ta có:

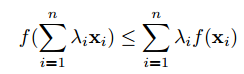
với $\lambda_i \ge 0$ và $\displaystyle \sum_{i=1}^n \lambda_i=1$ .
Đối với hàm lõm (concave function) thì ta đổi $\le$ thành $\ge$ . Ví dụ với hàm là hàm lõm ta có $\displaystyle \log(E_z(g(z))) \ge E_z \log(g(z))$ .
Sử dụng BĐT Jensen ta có:

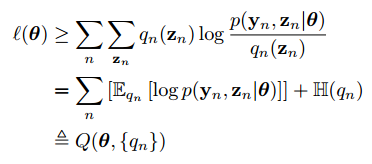
trong đó là phân phối xác suất của :
$\displaystyle H(q)=-\sum_z q(z)\log q(z)$
Biểu thức ở dòng cuối cùng được gọi là evidence lower bound hoặc ELBO. (ELBO sẽ được đề cập tiếp trong bài viết về Variational Autoencoder)
Thuật toán EM sẽ luân phiên việc tối đa lower bound wrt phân phối và tham số $\theta$

2. E step

Ta có:

trong đó

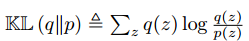
là Kullback-Leibler divergence giữa 2 phân phối xác suất và . Ta có $KL(p \parallel q) \ge 0$ và $KL(p \parallel q) = 0 \iff p=q$ .
DO đó ta có thể maximize lower bound $Q(\theta, q_n)$ wrt bằng cách cho $q_n^*= p(z_n|y_n, \theta)$ . Khi đó ta có:

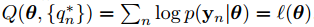
3. M step

Trong M step, ta cần maximize $Q(\theta,\{q_n\})$ wrt $\theta$ , với được tính ở E step ở iteration t. Do là hằng số đối với $\theta$ ta có thể bỏ trong bước M step. Ta thu được:

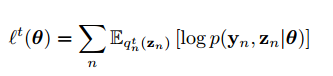
Biểu thức này được gọi là expected complete data log likelihood. Ta sẽ maximize hàm này để thu được

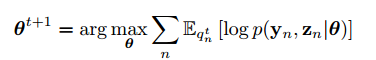
Tóm lại, thuật toán EM được viết dạng mã giả như sau (: mẫu dữ liệu, thông tin về bị ẩn).

Về ứng dụng của EM mình sẽ trình bày ở các bài tiếp theo.

III. Tài liệu tham khảo
```
  1. Probabilistic Machine Learning: An Introduction, by Kevin Patrick Murphy. MIT Press, 2021.     https://probml.github.io/pml-book/book1.html  
  2. http://uet.vnu.edu.vn/~tqlong/2016hmtk/em.pdf  
  3. https://machinelearningmastery.com/expectation-maximization-em-algorithm/  
```

III. Tài liệu tham khảo