Projected Gradient Descent

Ở các bài trước, chúng ta sử dụng gradient descent với miền của là $x \in \mathbb{R}^d$ . Khi miền $X \ne \mathbb{R}^d$ thì điểm cập nhật mới $x_{t+1}$ có thể không thuộc . Do đó sau mỗi bước cập nhật ta phải chiếu nó xuống để thu được điểm thuộc . Đây là một bài toán tối ưu có ràng buộc (constrained optimzation).

Trong bài này mình sẽ trình bày về Projected Gradient Descent.

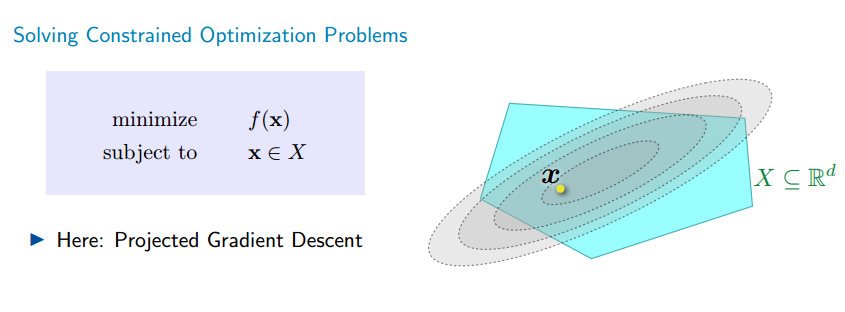
Sau mỗi lần cập nhật, thuật toán sẽ chiếu điểm xuống miền .

Ta có công thức cập nhật của projected gradient descent như sau:
$y_{t+1}=x_t - \eta\nabla f(x_t)$
$x_{t+1}=\Pi_X(y_{t+1})=\arg \min_{x \in X}\| x-y_{t+1}\|^2.$
Trước hết ta có một số tính chất sau:
Cho $X \subseteq \mathbb{R}^d$ là tập đóng và lồi. Cho $x \in X, y \in \mathbb{R}^d$ . Khi đó
i)) $(x-\Pi_X(y))^{T}(y- \Pi_X(y)) \le 0$
ii)) $\|x-\Pi_X(y)\|^2+\|y- \Pi_X(y)\|^2 \le \|x-y\|^2$
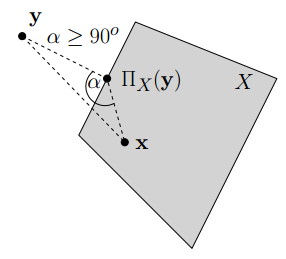
Chứng minh
Ta có bổ đề quan trọng sau:
Bổ đề: Cho hàm $f: dom(f) \rightarrow \mathbb{R}$ là hàm lồi và khả vi trên toàn miền $dom(f) \subseteq \mathbb{R}^d$ và cho $X \subseteq dom(f)$ là tập lồi. Điểm x^* được gọi là minimizer của trên toàn miền nếu và chỉ nếu $\nabla f(x^*)(x-x^*) \ge 0$ với mọi $x \in X$ .
i) Dễ thấy $\Pi_X(y)$ là minimizer của hàm lồi $d_y(x)=\|x-y\|^2$ trên miền . Sử dụng bổ đề trên ta có:
$\nabla d_y(\Pi_X(y))^T(x-\Pi_X(y)) \ge 0$
$\iff 2(\Pi_X(y)-y)^T(x-\Pi_X(y)) \ge 0$
$\iff (x-\Pi_X(y))^T(\Pi_X(y)-y) \le 0$ (đpcm)

ii) Đặt $v=x-\Pi_X(y), w=\Pi_X(y)-y$ . Sử dụng i) ta có
$0 \ge 2v^Tw= \|v\|^2 + \|w\|^2 +\|v-w\|^2= |x-\Pi_X(y)\|^2+\|y- \Pi_X(y)\|^2- \|x-y\|^2$ .
Suy ra $\|x-\Pi_X(y)\|^2+\|y- \Pi_X(y)\|^2 \le \|x-y\|^2$ (đpcm)
Việc phân tích tính hội tụ của Projected Gradient Descent trên các dạng hàm Lipschitz Convex Function, Smooth Convex Function, Smooth and Strongly Convex Function hoàn toàn tương tự ở các bài trước về Gradient Descent.

Tài liệu tham khảo

https://github.com/epfml/OptML_course
https://ee227c.github.io/
Stephen Boyd and Lieven Vandenberghe.
Convex Optimization.
Cambridge University Press, New York, NY, USA, 2004.