Về tính hội tụ của thuật toán Gradient Descent (Phần 3)

Ở bài cuối của chuỗi bài phân tích tính hội tụ của thuật toán Gradient Descent mình sẽ phân tích đối với hàm smooth và strongly convex function. Đây là 2 tính chất quan trọng kết hợp trong 1 hàm làm cho thuật toán gradient descent “faster”.
Định nghĩa: Cho hàm $f: dom(f) \rightarrow \mathbb{R}$ là hàm lồi và khả vi, $X \subseteq dom(f)$ lồi và $\mu \in \mathbb{R}^{+}$ . Hàm được gọi là strongly convex (với parameter $\mu$ ) trên nếu
$f(y) \ge f(x) + \nabla f(x)^T(y-x)+ \dfrac{\mu}{2}\|x-y\|^2$ , $\forall x, y \in X$ .
Nếu thì đơn giản gọi là strongly convex.
Hàm smooth convex đã được định nghĩa ở bài trước.
Dễ thấy rằng mọi hàm lồi đều thỏa mãn tính chất trên với $\mu=0$ .

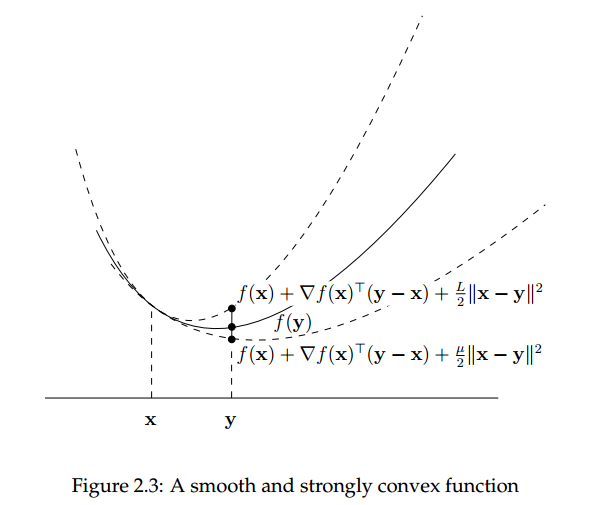
Ta có một số tính chất quan trọng sau của strongly convex function.

Bổ đề 1: Nếu hàm $f: \mathbb{R}^d \rightarrow \mathbb{R}$ strongly convex với tham số $\mu > 0$ thì strictly convex và có điểm global minimum duy nhất.
Bổ đề 2: Cho $f: \mathbb{R}^d \rightarrow \mathbb{R}$ strongly convex và smooth convex với tham số $\mu >0$ . Khi đó có dạng
$f(x)= \dfrac{\mu}{2}\|x-b\|^2 +c$ với $b \in \mathbb{R}^d, c \in \mathbb{R}$ .
Ta có có điểm global minimum duy nhất .
SỬ dụng biểu thức phần tích bài ở phần 1 và tính chất của strongly convex function
$g_t^T(x_t - x^*)= \nabla f(x_t)^T (x_t - x^*) \ge f(x_t)-f(x^*) +\dfrac{\mu}{2}\|x_t-x^*\|^2$ .
Ta được
$f(x_t)-f(x^*) \le \frac{1}{2\eta}(\eta^2\|\nabla f(x_t)\|^2 +\|x_t - x^*\|^2 -\|x_{t+1} - x^* \|^2)- \dfrac{\mu}{2}\|x_t - x^*\|^2$ (1)
Suy ra $\|x_{t+1} - x^*\| \le 2\eta(f(x^*) - f(x_t)) +\eta^2\|\nabla f(x_t)\|^2 +(1-\mu \eta)\|x_t - x^*\|^2$ (2)
Định lý: Cho hàm $f: \mathbb{R}^d \rightarrow \mathbb{R}$ là hàm lồi và khả vi. Giả sử hàm smooth với tham số và strongly convex với tham số $\mu$ . Theo bổ đề 1 ở trên, có điểm global minimum duy nhất . Chọn $\eta = \dfrac{1}{L}$ .
gradient descent với điểm bắt đầu bất kì ta có
i) $\|x_{t+1}- x^*\| \le (1- \dfrac{\mu}{L})\|x_t - x^*\|^2$ , $t \ge 0$ .
ii) Gọi là số vòng lặp tại một thời điểm nào đó.
$f(x_T) - f(x^*) \le \dfrac{L}{2}\bigg(1- \dfrac{\mu}{L}\bigg)^T\|x_0- x^*\|, T>0$ .

Chứng minh
i) Sử dụng định lý ở bài Phần 2 ta có $f(x^*) -f(x_t) \le f(x_{t+1}) -f(x^*) \le -\dfrac{1}{2L}\|\nabla f(x_t)\|^2$ .
Mà $\eta =\dfrac{1}{L}$ nên ta được $2\eta (f(x^*) -f (x_t)) +\eta^2\|\nabla f(x_t)\|^2 \le 0$ .
Từ 1) suy ra $\|x_{t+1}- x^*\| \le (1-\mu \eta)\|x_t - x^*\|^2 \le (1- \dfrac{\mu}{L})\|x_t - x^*\|^2$ (đpcm).
i)) Do smooth và $\nabla f(x^*)=0$ nên
$f(x_T) -f(x^*) \le \nabla f(x^*) (x_T- x^*) +\dfrac{L}{2}\|x_T - x^*\|^2 = \dfrac{L}{2}\|x_T - x^*\|^2$ .
Suy ra đpcm.
Từ đây cũng suy ra được $T \ge \dfrac{L}{\mu} \ln\bigg(\dfrac{R^2L}{2\epsilon}\bigg)$ , hay số iteration khoảng $O \bigg(\ln \bigg(\dfrac{1}{\epsilon} \bigg)\bigg)$ .
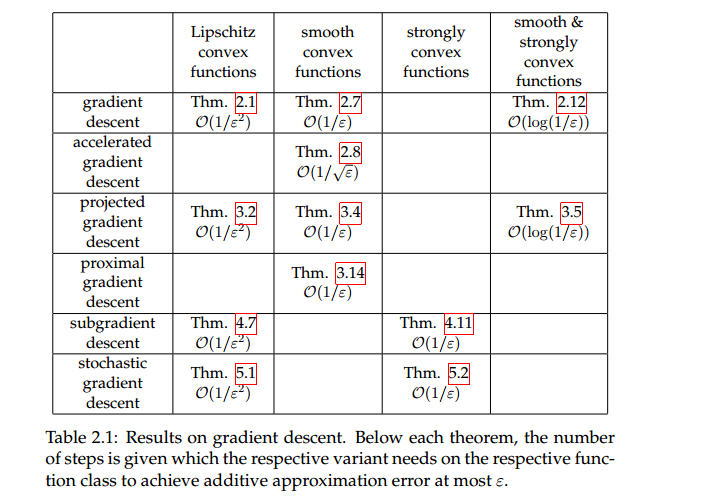
Bảng tổng kết

Tài liệu tham khảo

https://machinelearningcoban.com/
https://github.com/epfml/OptML_course
https://ee227c.github.io/
Stephen Boyd and Lieven Vandenberghe.
Convex Optimization.
Cambridge University Press, New York, NY, USA, 2004.
https://easyai.tech/en/ai-definition/gradient-descent/
https://towardsdatascience.com/binary-cross-entropy-and-logistic-regression-bf7098e75559?fbclid=IwAR1kSrG7pKJQvmge-M14CUkhjsZ0nlFA1Tw_4tBDWnBkBP8_fblXLrylk3s
http://www.seas.ucla.edu/~vandenbe/236C/lectures/gradient.pdf