Về tính hội tụ của thuật toán Gradient Descent (Phần 2)

Ở bài trước mình đã phân tính tính hội tụ của Gradient Descent đối với hàm Lipschitz Convex Function. Số steps khoảng $O\bigg(\dfrac{1}{\epsilon^2}\bigg)$ .
Bài viết này mình sẽ phân tích tính hội tụ của Gradient Descent với dạng hàm Smooth Convex Function.
(Có thể hình dung hàm này là “Not too curved”)
Nhắc lại tính chất first-order characterization of convexity của hàm lồi:
Với mọi $x, y \in dom(f)$ ta có $f(y) \ge f(x) +\nabla f(x)^T(y-x)$ .
Định nghĩa [smooth]: Cho hàm số $f: dom(f) \rightarrow \mathbb{R}$ là hàm khả vi, $X \subseteq dom(f)$ và $L \in \mathbb{R}^{+}$ . Hàm được gọi là “trơn” (smooth) (với tham số ) trên nếu
$f(y) \le f(x) + \nabla f(x)^T(y-x)+\dfrac{L}{2}\|x-y\|^2$ với mọi $x, y \in X$ .
Định nghĩa [smooth convex]: Cho hàm số $f: dom(f) \rightarrow \mathbb{R}$ là hàm lồi, khả vi, $X \subseteq dom(f)$ là tập lồi và $L \in \mathbb{R}^{+}$ . Hàm được gọi là “trơn lồi” (smooth convex) (với tham số ) trên nếu
$f(y) \le f(x) + \nabla f(x)^T(y-x)+\dfrac{L}{2}\|x-y\|^2$ với mọi $x, y \in X$ .
Với trường hợp thì ta có $f(y) = f(x) + \nabla f(x)^T(y-x)$ (do kết hợp với tính chất first-order characterization of convexity của hàm lồi) suy ra là hàm affine.
Lấy ví dụ với hàm là hàm lồi và dễ thấy rằng $f(y)=y^2=x^2+2x(y-x) + (x-y)^2= f(x) +f'(x)(y-x) +\dfrac{L}{2}(x-y)^2$ với . Do vậy hàm là hàm smooth convex với tham số .
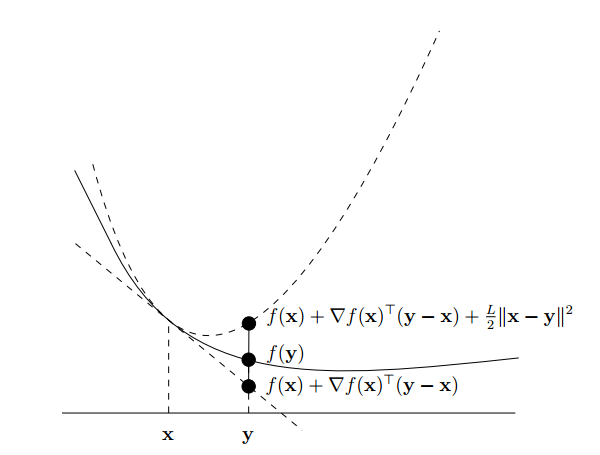
Hình sau minh họa hàm smooth convex.

Tổng quát hơn xét hàm bậc hai một biến f(x)=ax^2+bx+c với a>0 cũng là một hàm smooth convex với L=2a .
Có thể tự kiểm chứng với $f(y) = f(x) +f'(x)(y-x)+\dfrac{L}{2}(x-y)^2$ với L=2a .
Còn với biến là một vector, dạng toàn phương (quadratic form) có dạng f(x)=x^TAx+b^Tx+c với là ma trận đối xứng và nửa xác định dương thì hàm này có phải là hàm smooth convex không? Câu trả lời là có.
Ta có định lý sau:
Định lý: Cho hàm f(x)= x^TQx+b^Tx+c trong đó là ma trận nửa xác định dương, đối xứng, $Q \in \mathbb{R}^{d \times d}, b \in \mathbb{R}^{d}, c \in \mathbb{R}$ . Khi đó smooth convex với tham số $2\|Q\|$ , trong đó $\|Q\|$ là spectral norm của .
Về spectral norm của ma trận được định nghĩa như sau:
Định nghĩa [spectral norm of matrix]. Cho ma trận $A \in \mathbb{R}^{m \times n}$ . Khi đó
$\|A\|:= \max_{v \in \mathbb{R}^n, v \ne 0} \dfrac{\|Av\|}{\|v\|}= \max_{\|v\|=1}\|Av\|$
được gọi là 2-norm hay spectral norm của .
Lưu ý: spectral norm này khác với Frobenius norm của ma trận.
Chứng minh
Do là ma trận đối xứng, nửa xác định dương nên f(x) là hàm lồi. Hơn nữa ta cũng có x^TQy=y^TQx với x, y bất kỳ. Khi đó có thể viết lại
$f(y)=y^TQy=x^TQx+2x^TQ(y-x)+(x-y)^TQ(x-y)= \\ f(x)+ 2x^TQ(y-x)+(x-y)^TQ(x-y)$

Sử dụng bất đẳng thức Cauchy-Schwarz và tính chất của spectral norm ta có
$(x-y)^TQ(x-y) \le \|x-y\|\|Q(x-y)\|\le \|x-y\|\|Q\|\|x-y\|=\|Q\|\|x-y\|^2$
Suy ra $f(y) \le f(x) +2x^TQ(y-x) + \|Q\|\|x-y\|^2$ . Mà $\nabla f(x) =2x^TQ$ . Do đó
$f(y) \le f(x) + \nabla f(x)(y-x) +\dfrac{2\|Q\|}{2}\|x-y\|^2$ . Điều này chứng tỏ smooth với tham số $2\|Q\|$

Tiếp theo là một định lý về hàm smooth convex.
Định lý: Cho $f: \mathbb{R}^d \rightarrow \mathbb{R}$ là hàm lồi, khả vi. Hai mệnh đề sau là tương đương.
i) smooth với tham số .
ii) $\|\nabla f(x)- \nabla f(y)| \le L\|x-y\|$ với mọi $x, y \in \mathbb{R}^d$ .
Chứng minh:
Sử dụng tính chất của tập lồi, xét $x, y \in dom(f)$ thì ty+(1-t)x = x +t(y-x) cũng thuộc dom(f) với $t \in [0,1]$ .
Xét hàm g(t)=f(x+t(y-x))) . Giả sử ta có ii) thì ta có:
$g'(t) - g'(0)= (\nabla f(x+t(y-x))- \nabla f(x))^T(y-x) \le tL\|x-y\|^2$
Lấy tích phân từ t=0 đến t=1 ta có:
$f(y) = g(1) = g(0)+ \displaystyle \int_{0}^1 g'(t)dt \le g'(0) + \dfrac{L}{2}\|x-y\|^2 = \\ f(x) + \nabla f(x)^T(y-x) + \dfrac{L}{2}\|x-y\|^2$ .
Từ đây suy ra smooth convex với tham số .
Ngược lại nếu ta có i) tức là $f(y) \le f(x) + \nabla f(x)^T(y-x) + \dfrac{L}{2}\|x-y\|^2$ .
Hoán đổi x, y ta được $f(x) \le f(y) + \nabla f(y)^T(x-y) + \dfrac{L}{2}\|y-x\|^2$ .
Từ đây dễ dàng suy ra $\|\nabla f(x)- \nabla f(y)| \le L\|x-y\|$ .
Như vậy i) và i)) tương đương nhau.
Định lý: Cho hàm $f: \mathbb{R}^d \rightarrow \mathbb{R}$ khả vi và trơn với tham số . Với learning rate $\eta =\dfrac{1}{L}$ khi áp dụng thuật toán gradient descent ta có
$f(x_{t+1}) \le f(x_t)-\dfrac{1}{2L}\|\nabla f(x_t)\|^2$ , $t \ge 0$
Chứng minh
Với learning rate $\eta =\dfrac{1}{L}$ thì theo công thức cập nhật của gradient descent ta có $x_{t+1}-x_t= -\dfrac{\nabla f(x_t)}{L}$ và áp dụng công thức hàm trơn:
$f(x_{t+1}) \le f(x_t) + \nabla f(x_t)^T(x_{t+1}-x_t) + \dfrac{L}{2}\|x_t -x_{t+1}\|^2 \\ = f(x_t) -\dfrac{1}{L}\|\nabla f(x_t)\|^2+\dfrac{1}{2L}\|\nabla f(x_t)\|^2\\ = f(x_t) - \dfrac{1}{2L}\|\nabla f(x_t)\|^2$
Sau đây là định lý về sự hội tụ của gradient descent với hàm smooth convex.
Định lý: Cho hàm $f: \mathbb{R}^d \rightarrow \mathbb{R}$ lồi, khả vi với điểm global minimum là x^* , giả sử trơn với tham số . Với learning rate $\eta = \dfrac{1}{L}$ khi áp dụng gradient descent ta có:
$f(x_T)-f(x^*) \le \dfrac{L}{2T}\|x_0 - x^*\|^2$ , T>0
Chứng minh
Áp dụng định lý trên và lấy tổng từ $0 \rightarrow T-1$ ta có
$\displaystyle \dfrac{1}{2L} \sum_{t=0}^{T-1}\|\nabla f(x_t)\|^2 \le \sum_{t=0}^{T-1} (f(x_t) - f(x_{t+1})) = f(x_0) -f(x_T)$ .
Với $\eta = \dfrac{1}{L}$ và áp dụng phân tích đã có trong bài Về tính hội tụ của thuật toán Gradient Descent (Phần 1) ta có:
$\displaystyle \sum_{t=0}^{T-1}(f(x_t) - f(x^*)) \le \dfrac{1}{2L}\sum_{t=0}^{T-1}\|\nabla f(x_t)\|^2 +\dfrac{L}{2}\|x_0 - x^*\|$ hay
$\displaystyle \sum_{t=1}^{T}(f(x_t) - f(x^*)) \le \dfrac{L}{2}\|x_0 - x^*\|$ .
Mặc khác do $f(x_{t+1}) \le f(x_t)$ với $0 \le t \le T$ nên
$f(x_T) -f(x^*)\le \dfrac{1}{T} \sum_{t=1}^{T}(f(x_t) - f(x^*)) \le \dfrac{L}{2T}\|x_0 - x^*\|^2$ .
Giả sử khoảng cách giữa điểm khởi tạo và điểm global minimum là , tức là $\|x_0 - x^*\| =R$ . Khi đó ta cần $T \ge \dfrac{R^2L}{2\epsilon}$ để khoảng cách error là $\epsilon$ .
Ta thấy số vòng lặp ít nhất phụ thuộc vào cả và $\epsilon$ .
Từ đây ta ước lượng số vòng lặp với hàm smooth convex khoảng $O\bigg(\dfrac{1}{\epsilon}\bigg)$ . Nhanh hơn so với hàm Lipschitz convex.
Đặc biệt với hàm f(x)=x^2 hay tổng quát hơn f(x)=ax^2+bx+c là hàm smooth convex với tham số L=2a nên nếu chọn learning rate là $\eta =\dfrac{1}{L}$ thì chỉ cần sau một vòng lặp thì gradient descent đã hội tụ đúng điểm tối ưu. Vì khi đó với $t\ge 1$ thì $f(x_t)=f(x_{t+1})= f(x^*)$ .

Tài liệu tham khảo

https://machinelearningcoban.com/
https://github.com/epfml/OptML_course
https://ee227c.github.io/
Stephen Boyd and Lieven Vandenberghe.
Convex Optimization.
Cambridge University Press, New York, NY, USA, 2004.
https://easyai.tech/en/ai-definition/gradient-descent/
https://towardsdatascience.com/binary-cross-entropy-and-logistic-regression-bf7098e75559?fbclid=IwAR1kSrG7pKJQvmge-M14CUkhjsZ0nlFA1Tw_4tBDWnBkBP8_fblXLrylk3s
http://www.seas.ucla.edu/~vandenbe/236C/lectures/gradient.pdf