Về tính hội tụ của thuật toán Gradient Descent (Phần 1)

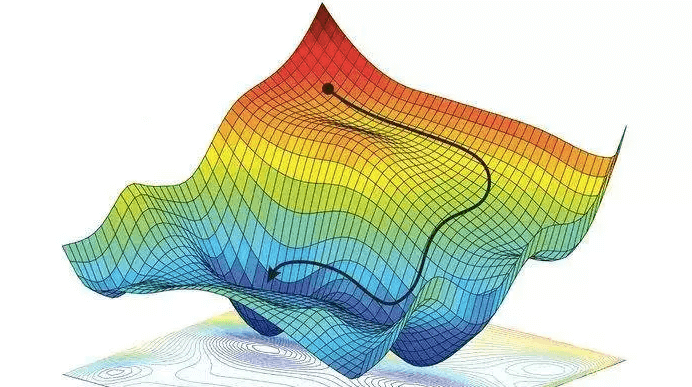
Trong bài toán tối ưu cụ thể là các bài toán tìm giá trị lớn nhất hay giá trị nhỏ nhất của một hàm số, ta thường đi giải phương trình đạo hàm hoặc đạo hàm riêng bằng 0 đối với hàm nhiều biến. Tuy nhiên, việc tối ưu hàm lỗi trong Machine Learning gặp phải các vấn đề sau:
- Với những tập dữ liệu lớn, nhiều chiều thì sẽ gây ra tốn bộ nhớ của máy tính và tính toán chậm chạp. Ví dụ công thức tính tham số của thuật toán Linear Regression như sau $w=(X^{T}X)^{\dagger}X^{T}y$ (kí hiệu $A^{\dagger}$ là ma trận giả nghịch đảo). Khi đó nếu dữ liệu train lớn và chiều của dữ liệu lớn thì kích thước ma trận sẽ lớn, việc tính nghịch đảo và nhân ma trận sẽ chậm.
- Trong nhiều thuật toán Machine Learning các hàm lỗi (Loss Function) đôi khi rất phức tạp nên việc tính đạo hàm là không khả thi.
  Và thuật toán Gradient Descent sẽ giải quyết hai vấn đề nêu trên.
Ý tưởng của Gradient Descent là giá trị hàm số sẽ giảm nhanh nhất khi đi ngược hướng đạo hàm.
Công thức cập nhật trọng số: $\theta = \theta - \eta \nabla_{\theta} f(\theta)$ với $\theta$ là tham số mô hình và $\eta$ gọi là tốc độ học (learning rate).
Chi tiết rõ hơn về thuật toán, các biến thể và cách cài đặt có thể xem tại Blog Machine Learning cơ bản
Ở bài này mình sẽ phân tích tính hội tụ của Gradient Descent, số lần lặp tối thiểu để thuật toán hội tụ và tốc độ hội tụ của từng dạng hàm số (các hàm được đề cập đều có tính chất chung là hàm lồi). Trước tiên ta đi qua một số kiến thức chuẩn bị.

I. Một số kiến thức chuẩn bị

1. Lý thuyết về tập lồi, hàm lồi

Một tập được gọi là tập lồi nếu mọi điểm trên đoạn thẳng nối 2 điểm bất kỳ trong tập đều thuộc tập hợp . Tức là, với 2 điểm bất kỳ $x, y \in C$ và với $0 \le \lambda \le 1$ ta có $\lambda x + (1-\lambda)y \in C$ .
Ví dụ tập lồi
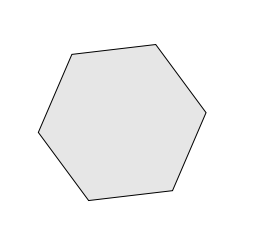
Ví dụ tập không lồi
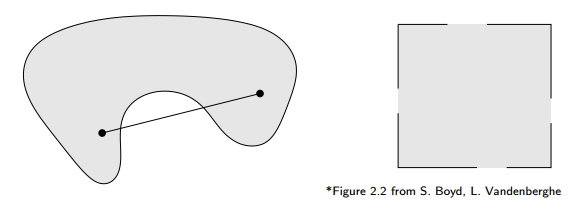
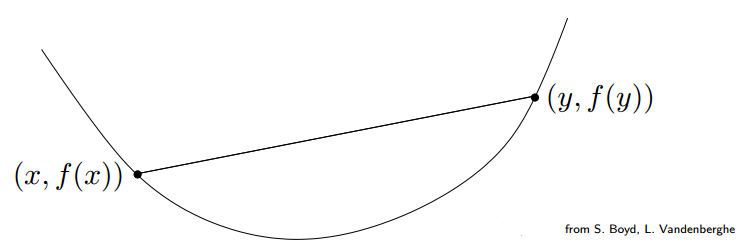
Một hàm $f: \mathbb{R}^{d} \rightarrow \mathbb{R}$ được gọi là hàm lồi nếu miền xác định của , là một tập lồi và với mọi $x, y \in dom(f)$ và $\lamba, 0 \le \lambda \le 1$ ta có
$f(\lambda x +(1- \lambda) y) \le \lambda f(x) + (1- \lambda)f(y)$ .
Một cách hình học: Đoạn thẳng nối giữa nằm trên đồ thị của .
[Hàm lồi chặt - Strictly Convex Function]. Hàm $f: dom(f) \rightarrow \mathbb{R}$ là hàm lồi chặt nếu lồi và với mọi $x \ne y \in dom(f)$ và với mọi $\lambda \in (0, 1)$ , ta có
$f(\lambda x +(1- \lambda) y) < \lambda f(x) + (1- \lambda)f(y)$
Một số hàm lồi
- Linear functions:
- Affine functions:
- Exponential: $f(x)=e^{\alpha x}$
- Norms: Mọi norm trên $\mathbb{R}^d$ đều là hàm lồi.
  Ví dụ xét tính lồi của $\|x\|$ . Sử dụng tính chất của norm là bất đẳng thức tam giác $\|x+y\| \le \|x\| + \|y\|$ và $\|ax\| =a\|x\|$ với là số thực.
  Ta có $\| \lambda x+ (1-\lambda)y\| \le \|\lambda x\|+ \|(1-\lambda) y\|= \lambda \|x\|+ (1-\lambda)\|y\|$ . Do vậy norm là một hàm lồi.

2. Kiểm tra tính chất lồi dựa vào đạo hàm bậc nhất (First-order characterization of convexity)

Định lý: Giả sử hàm số có tập xác định , có đạo hàm tại mọi điểm trên tập xác định, hay vector gradient của là $\nabla f := \bigg(\dfrac{\partial f}{\partial x_1}(x),..., \dfrac{\partial f}{\partial x_d}(x)\bigg)$ tồn tại với mọi $x \in dom(f)$ . Khi đó hàm lồi nếu và chỉ nếu lồi và $f(y) \ge f(x)+ \nabla f(x)^T(y-x)$ với mọi $x, y \in dom(f)$ .
Một cách trực quan: Hàm số là lồi nếu mặt tiếp tuyến tại một điểm bất kỳ trên đồ thị hàm số không nằm trên đồ thị đó.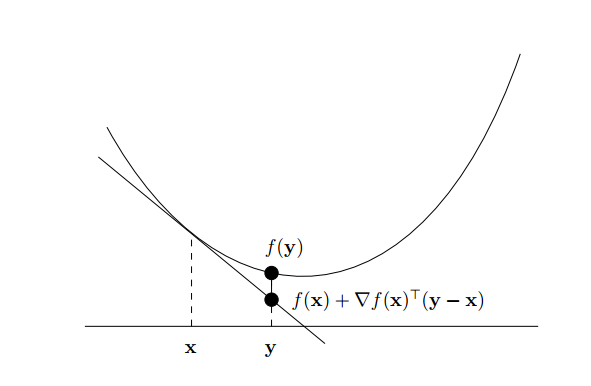

3. Kiểm tra tính chất lồi dựa vào đạo hàm bậc hai (Second-order characterization of convexity)

Hàm $f: dom(f) \rightarrow \mathbb{R}$ được gọi là twice continuously differentiable nếu $\nabla f$ có đạo hàm (differentiable) và $\nabla^2 f$ liên tục (continuous).
Định lý: Giả sử hàm số có tập xác định , và twice continuously differentiable và ma trận Hessian của

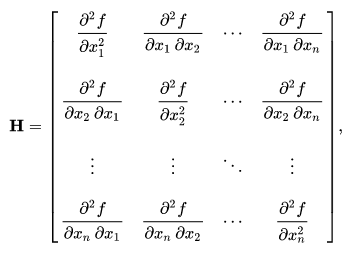
là ma trận đối xứng và tồn tại với mọi $x\in dom(f)$ . Khi đó là hàm lồi nếu và chỉ nếu lồi và với mọi $x \in dom(f)$ ta có $H \succeq0$ , hay là ma trận nửa xác định dương. Nếu là hàm lồi chặt thì là ma trận xác định dương.

4. Local Minimum và Global Minimum

Vấn đề của Gradient Descent là nó chỉ tìm được một điểm cực tiểu local minimum và ta không biết được điểm đó có phải là global minimum hay không. Tuy nhiên có một tính chất qua trọng sau: Nếu hàm số đó làm hàm lồi (convex) thì local minimum đó cũng chính là global minimum, tính chất này sẽ chứng minh sau đây.
Định nghĩa: Một local minimum (điểm tối ưu cục bộ) của hàm $f: dom(f) \rightarrow \mathbb{R}$ là điểm sao cho tồn tại $\epsilon > 0$ với $f(x) \le f(y)$ với mọi $y \in dom(f)$ thỏa mãn $\|y-x\| < \epsilon$ .
Định lý: Gọi là local minimum của hàm lồi $f: dom(f) \rightarrow \mathbb{R}$ . Khi đó cũng là global minimum (tối ưu toàn cục), nghĩa là $f(x^*) \le f(y)$ với mọi $y \in dom(f)$ .
Chứng minh: Giả sử rằng tồn tại $y \in dom(f)$ sao cho .
Đặt $y':= \lambda x^* +(1-\lambda)y$ với $\lambda \in (0, 1)$ .
Từ tính chất của hàm lồi ta có:
$f(y')=f(\lambda x^* +(1-\lambda)y) \le \lambda f(x^*)+ (1-\lambda)f(y) < \lambda f(x^*)+ (1-\lambda)f(x^*)= f(x^*)$
Do đó . Chọn $\lambda$ càng gần 1 thì $\|y'-x^*\| < \epsilon$ . Điều này mẫu thuẫn với là local minimum.
Từ đây suy ra điều phải chứng minh.
Để ý thấy hàm Mean Square Error (MSE) trong Linear Regression hay Cross Entropy trong Logistic Regression đều là các hàm lồi. Các bạn có thể tự kiểm chứng điều này hoặc xem tại Binary cross-entropy and logistic regression. Khi đó dùng thuật toán tối ưu Gradient Descent thì sẽ tìm được điểm tối ưu toàn cục.
Thường các hàm lỗi trong Deep Neural Network là các hàm non-convex và đây là vấn đề của Non-convex Optimization.
Định lý: Cho $f: dom(f) \rightarrow \mathbb{R}$ là hàm lồi và có đạo hàm trên toàn miền xác định. Cho $x \in dom(f)$ . Khi đó nếu $\nabla f(x)=0$ thì là global minimum.
Định lý: Cho $f: dom(f) \rightarrow \mathbb{R}$ là hàm lồi chặt (strictly convex). Khi đó có điểm global minimum duy nhất.

II. Phân tích tính hội tụ của Gradient Descent

Cho hàm $f: \mathbb{R}^d \rightarrow \mathbb{R}$ có đạo hàm và là hàm lồi. Giả sử rằng có điểm global minimum x^* và mục tiêu là đi tìm (hoặc xấp xỉ) x^* , nghĩa là với $\epsilon >0$ cho trước, ta cần tìm $x \in \mathbb{R}^d$ sao cho $f(x)-f(x^*) < \epsilon$ .
Nhắc lại công thức cập nhật của Gradient Descent $\theta = \theta - \eta \nabla_{\theta} f(\theta)$ hay viết lại $x_{t+1}:=x_t - \eta \nabla f(x_t)$ . Chúng ta muốn tìm số vòng lặp (số lần cập nhật) nhỏ nhất mà thỏa mãn $f(x_t)-f(x^*) < \epsilon$ .

Phần đầu tiên chúng ta tiếp cận với hàm Lipschitz Convex Function

Định nghĩa: (L-Lipschitz). Một hàm $f: \Omega \rightarrow \mathbb{R}$ được gọi là L-Lipschitz nếu với mọi $x, y \in \Omega$ ta có $\|f(x)-f(y)\| \le L\|x-y\|$ .
Định lý: Nếu hàm là L-Lipschitz, có đạo hàm và là hàm lồi, thì $\|\nabla f(x)\| \le L$ với mọi $x \in \Omega$ .
Định lý: Cho $f: \mathbb{R}^d \rightarrow \mathbb{R}$ là hàm lồi, có đạo hàm và L-Lipschitz trên toàn miền xác định của , có global minimum . Hơn nữa, giả sử $\|x_0 - x^*\| \le R$ ( là điểm khởi tạo ban đầu) và $\|\nabla f(x)\| \le L$ với mọi . Chọn learning rate $\eta =\dfrac{R}{L\sqrt{T}}$ . Gọi $x_1, x_2,.., x_{T-1}$ là dãy các giá trị được tính bằng công thức cập nhật của Gradient Descent với $\eta =\dfrac{R}{L\sqrt{T}}$ .
Khi đó ta có $f\bigg(\dfrac{1}{T}\displaystyle \sum_{t=0}^{T-1}x_t\bigg) - f(x^*) \le \dfrac{RL}{\sqrt{T}}$ .
Chứng minh:
Đặt $g_t =\nabla f(x_t)$ . Khi đó $g_t = \dfrac{x_t-x_{t+1}}{\eta}$
$g_t^T(x_t - x^*)= \dfrac{1}{\eta}(x_t -x_{t+1})^T(x_t - x^*)$ .
Áp dụng công thức $2v^Tw = \|v\|^2 +\|w\|^2- \|v-w\|^2$ với .
Ta có $g_t^T(x_t - x^*)=\dfrac{1}{2\eta}(\|x_t - x_{t+1}\|^2 +\|x_t - x^*\|^2 -\|x_{t+1}-x ^*\|^2)=$ $\dfrac{1}{2\eta}(\eta^2\|g_t\|^2 +\|x_t - x^*\|^2 -\|x_{t+1}-x ^*\|^2)=$ $\dfrac{\eta}{2}\|g_t\|^2 +\dfrac{1}{2\eta}(\|x_t - x^*\|^2 -\|x_{t+1}-x ^*\|^2)$ .
Lấy tổng trên lần cập nhật đầu tiên:
$\displaystyle \sum_{t=0}^{T-1}g_t^T(x_t - x^*)= \dfrac{\eta}{2}\sum_{t=0}^{T-1}\|g_t\|^2 + \dfrac{1}{2\eta}(\|x_0 - x^*\|^2 -\|x_{T}-x ^*\|^2)$
Sử dụng tính chất first-order characterization of convexity ta có:
$f(y) \ge f(x)+ \nabla f(x)^T(y-x)$ với mọi .
Chọn ta được $f(x_t) -f (x^*) \le g_t^T(x_t - x^*)$ .
Khi đó $\displaystyle \sum_{t=0}^{T-1}(f(x_t)-f(x^*)) \le \dfrac{\eta}{2}\sum_{t=0}^{T-1}\|g_t\|^2 +\dfrac{1}{2\eta}\|x_0 - x^*\|^2$ .
Biểu thức này gọi là chặn trên của trung bình lỗi trên tất cả các lần cập nhật.
Do $\|x_0 - x^*\|\le R$ và $\|g_t\| \le L$ nên
$\displaystyle \sum_{t=0}^{T-1}(f(x_t)-f(x^*)) \le \dfrac{\eta}{2}\sum_{t=0}^{T-1}\|g_t\|^2 +\dfrac{1}{2\eta}\|x_0 - x^*\|^2$
$\le \dfrac{\eta}{2}L^2T+\dfrac{1}{2\eta}R^2$ .
Xét hàm $h(\eta)= \dfrac{\eta}{2}L^2T+\dfrac{R^2}{2\eta}$ .
Ta chọn $\eta$ sao cho đạt giá trị nhỏ nhất.
Giải phương trình đạo hàm $q'(\eta)=0$ được $\eta=\dfrac{R}{L\sqrt{T}}$ và $h(\dfrac{R}{L\sqrt{T}})= \dfrac{RL}{\sqrt{T}}$ .
Từ đây dễ thấy với $T \ge \dfrac{R^2L^2}{\epsilon^2}$ thì average error $\le$ $\dfrac{RL}{\sqrt{T}} \le \epsilon$ .
Và do là hàm lồi nên $f\bigg(\dfrac{1}{T}\displaystyle \sum_{t=0}^{T-1}x_t\bigg) - f(x^*) \le \dfrac{RL}{\sqrt{T}} \blacksquare$ .
Suy ra số lần cập nhật của Gradient Descent đối với hàm Lipschitz Convex Function là khoảng $O\bigg(\dfrac{1}{\epsilon^2}\bigg)$ với $\epsilon>0$ bất kỳ cho trước.
Ở bài sau mình sẽ nói về tốc độ hội tụ của Gradient Descent trên các hàm Smooth Convex Function và Strongly Convex Function.

III. Tài liệu tham khảo

https://machinelearningcoban.com/
https://github.com/epfml/OptML_course
https://ee227c.github.io/
Stephen Boyd and Lieven Vandenberghe.
Convex Optimization.
Cambridge University Press, New York, NY, USA, 2004.
https://easyai.tech/en/ai-definition/gradient-descent/
https://towardsdatascience.com/binary-cross-entropy-and-logistic-regression-bf7098e75559?fbclid=IwAR1kSrG7pKJQvmge-M14CUkhjsZ0nlFA1Tw_4tBDWnBkBP8_fblXLrylk3s