Ở bài trước mình đã nói về Cholesky Decomposition, bài này mình sẽ trình bày về QR Decomposition.

I. Các khái niệm cơ bản

1. Tích vô hướng và không gian Euclid

Cho là không gian vector. Ánh xạ
$\langle, \rangle: V \times V \rightarrow \mathbb{R}$
$\hspace{3mm}$ $(u, v) \rightarrow \langle u, v\rangle$
được gọi là tích vô hướng trong nếu với mọi $u, v, w \in V$ và $\alpha, \beta \in \mathbb{R}$ , thỏa các tính chất sau:
$\textbf{(i)} \langle \alpha u +\beta v, w \rangle = \alpha\langle u, w \rangle + \beta\langle v, w \rangle$ ;
$\textbf{(ii)} \langle w, \alpha u +\beta v\rangle = \alpha\langle u, w \rangle + \beta\langle v, w \rangle$ ;
$\textbf{(iii)} \langle u, v\rangle= \langle v, u\rangle$ ;
$\textbf{(iv)} \langle u, u\rangle\ge 0$ trong đó $\langle u, u\rangle = 0 \iff u=0$ .
Định nghĩa. Ta gọi một không gian vector hữu hạn chiều với tích vô hướng là một không gian Euclid.
Cho không gian vector $V = \mathbb{R}^n$ với , ta định nghĩa $\langle u, v\rangle:= x_1y_1+x_2y_2+...+x_ny_n$ .
Khi đó là không gian Euclid. Tích vô hướng này được gọi là tích vô hướng chính tắc trong $\mathbb{R}^n$ .
[Bất đẳng thức Cauchy - Schwarz]. Với mọi $u, v \in V$ ta có
$\langle u, v\rangle \le \|u \|^2 \|v\|^2$ .
Dấu xảy ra khi và chỉ khi phụ thuộc tuyến tính.
[Bất đẳng thức tam giác]. Với mọi $u, v \in V$ ta có
$\|u+v \| \le \|u\| + \|v \|$ .
Dấu xảy ra khi và chỉ khi tồn tại $\lambda \ge 0$ sao cho $v= \lambda u$ .
Định nghĩa. Cho là không gian Euclid và $u, v \in V$ . Góc giữa hai vector là $\theta \in[0, \pi]$ thỏa $cos\theta= \dfrac{\langle u, v\rangle}{\|u\|\|v\|}$
2. Cơ sở trực giao và cơ sở trực chuẩn, quá trình trực chuẩn hóa Gram-Schmidt

Giả sử trên trang bị một tích vô hướng. Hai vector được gọi là trực giao, ký hiệu $x \perp y$ nếu $\langle x, y\rangle=0$ .
Hệ vector $\{e_1, e_2,...,e_m\}$ trong gọi là hệ trực giao nếu $e_i \ne 0$ và $e_i \perp e_j$ với mọi $i \ne j, i, j= \overline{1,m}$ , tức là
$\langle e_i, e_j \rangle= 0$ nếu $i \ne j$ và $\langle e_i, e_j \rangle = \|e_i\|^2$ nếu .
Hệ trực giao mà $\|e_i\|=1$ gọi là hệ trực chuẩn.
Hệ trực giao là hệ độc lập tuyến tính.
Cơ sở gọi là một cơ sở trực giao (trực chuẩn) nếu nó là một hệ trực giao (trực chuẩn).
Định lý [Gram - Schmidt]. Nếu hệ các vector $\{v_1,v_2,...,v_m\}$ là độc lập tuyến tính bất kỳ trong thì tồn tại hệ trực chuẩn $\{e_1,e_2,...,e_m \}$ sao cho $e_i \in span\{v_1,...,v_i\}, i= \overline{1,m}$ .
Ta chứng minh bằng quy nạp.
Với đặt $e_1=\dfrac{v_1}{\|v_1\|}$ . Giả sử xây dựng được hệ $\{e_1,...,e_j\}$ trực chuẩn và $e_k \in span\{v_1,...,v_k\}, \forakk k \in \overline{1,j}$ . Ta chỉ ra cách xây dựng $e_{j+1}$ .
Đặt $e'_{j+1}=v_{j+1}+\alpha_1e_1+...+\alpha_je_j$ , các $\alpha_i$ xác định sau và $e'_{j+1} \perp e_k, \forakk k \in \overline{1,j}$ .
Ta có $\langle e'_{j+1}, e_k \rangle=0 \iff \langle v_{j+1}, e_k \rangle +\alpha_k \|e_k\|^2=0$ .
Mà $\|e_k\|=1$ nên $\alpha_k=-\langle v_{j+1}, e_k \rangle$ hay $\displaystyle e'_{j+1}=v_{j+1} -\sum_{k=1}^j \langle v_{j+1}, e_k \rangle e_k$
Vì $\{v_1,..., v_j, v_{j+1}\}$ độc lập tuyến tính nên $v_{j+1}$ không biểu diễn tuyến tính qua $\{e_1,...,e_j\}$ , vì $span\{e_1,...,e_j\}= span\{v_1,.., v_j\}$ , do đó $e_{j+1}\ne 0$ .
Đặt $e_{j+1}=\dfrac{e'_{j+1}}{\|e'_{j+1}\|}$ . Ta được hệ trực chuẩn thỏa mãn định lý.
Hệ quả: Nếu là một cơ sở bất kỳ của thì tồn tại cơ sở trực chuẩn sao cho $e_j \in span\{v_1,..,v_j\}$ .
Định lý: Nếu là một cơ sở trực chuẩn của thì với mọi $x \in V$ ta có $\displaystyle x=\sum_{i=1}^n\langle x, e_i \rangle e_i$ .
Giả sử .
$\implies \langle x, e_i \rangle=x_1\langle e_1, e_i \rangle+ x_2\langle e_2, e_i \rangle+...+ x_n\langle e_n, e_i \rangle$ .
Vì là cơ sở trực chuẩn nên $\langle u_i, u_j \rangle=0$ nếu $i\ne j$ và $\langle u_i, u_j \rangle=1$ nếu .
Suy ra $\langle u_i, u_j \rangle=x_i$ .
Ví dụ: Trực chuẩn hóa Gram - Schmidt hệ vector

II. Phân tích QR

1. Phát biểu

Giả sử rằng $A \in M_{n \times m}(\mathbb{R})$ là ma trận gồm cột độc lập tuyến tính, viết dưới dạng các vector cột là . Trực chuẩn hóa các vector ta được các vector . Mặc khác từ định lý nêu ở trên ta có
$\displaystyle v_k=\sum_{i=1}^k \langle v_k, e_i \rangle e_i$
Vì vậy ta có
$A=(v_1, v_2,..., v_m)=(e_1, e_2,..., e_m)\left( \begin{matrix} \langle v_1, e_1 \rangle & \langle v_2, e_1 \rangle & \cdots & \langle v_m, e_1 \rangle \\ 0 & \langle v_2, e_2 \rangle & \cdots & \langle v_m, e_2 \rangle \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & \langle v_m, e_m \rangle \\ \end{matrix} \right)= QR$
với là ma trận có các cột trực giao, là ma trận tam giác trên vuông cấp
[Định lý]. Giả sử rằng $A \in M_{n \times m}(\mathbb{R})$ có các cột độc lập tuyến tính, khi đó ta có thể phân tích trong đó là ma trận trực giao và là ma trận tam giác trên cấp khả nghịch.
Ví dụ: Cho ma trận
$A=(v_1, v_2, v_3)=\begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{pmatrix}$

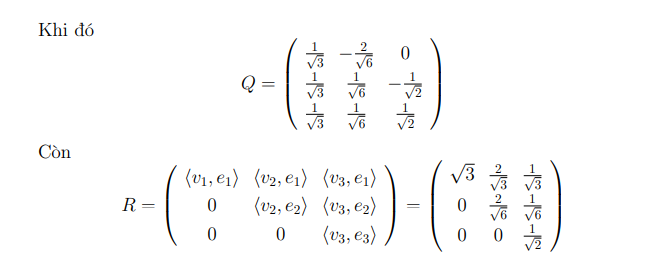
2. Code Python

import numpy as np

#Chuẩn hóa vector
def normalize(vector):
    norm_vector=np.linalg.norm(vector)
    return vector/norm_vector

#Tìm ma trận trực giao Q bằng Gram - Schmidt Process
def GramSchmidtProcess(A):
    A=np.transpose(A)
    n=A.shape[1]
    B=np.zeros((n,n), dtype=np.float32)
    e_1=normalize(A[:,0])
    B[:,0]=e_1
    for i in range(1,n):
        temp=0
        for j in range(0,i):
            temp=temp+(np.inner(A[:,i],B[:,j]))*B[:,j]
        temp2=normalize(A[:,i]-temp)
        B[:,i]=temp2
    return B

#Cách 1: Tính R bằng ma trận nghịch đảo
#A=QR => R=Q^-1.dot(A)
def QR_Decomposition_GramSchimidt_1(A):
    Q=GramSchmidtProcess(A)
    R=(Q.T).dot(A.T)
    return Q,R
    
#Cách 2
def QR_Decomposition_GramSchmidt_2(A):
    Q=GramSchmidtProcess(A)
    A=np.transpose(A)
    m=A.shape[0]
    R=np.zeros((m,m))
    for i in range(0, m):
        for j in range(0, i+1):
            R[j][i]=np.inner(A[:,i], Q[:,j])
    return Q,R

A=np.array([[1,1,1],[0,1,1],[0,0,1]])
Q,R=QR_Decomposition_GramSchmidt_2(A)
print(Q)
print(R)

[[ 5.7735026e-01 -8.1649655e-01  4.2146848e-08]
 [ 5.7735026e-01  4.0824834e-01 -7.0710677e-01]
 [ 5.7735026e-01  4.0824834e-01  7.0710677e-01]]
[[1.73205078 1.15470052 0.57735026]
 [0.         0.81649667 0.40824834]
 [0.         0.         0.70710677]]

Kết quả cho ra đúng với kết quả ta làm ở trên.

III. Tài liệu tham khảo

Slide bài giảng Đại số A2, Thầy Lê Văn Luyện, ĐH KHTN TPHCM.
https://fit.mta.edu.vn/files/DanhSach/BaigiangDSTT_16.pdf

I. Các khái niệm cơ bản

1. Tích vô hướng và không gian Euclid

2. Cơ sở trực giao và cơ sở trực chuẩn, quá trình trực chuẩn hóa Gram-Schmidt

II. Phân tích QR

1. Phát biểu

2. Code Python

III. Tài liệu tham khảo