Bài trước mình đã nói về LU Decomposition, ở bài này mình sẽ trình bày về Cholesky Decomposition. Phân tích này được đề xuất bởi nhà toán học André-Louis Cholesky, nó có nhiều ứng dụng trong tính ma trận nghịch đảo, giải hệ phương trình tuyến tính, tính định thức, Least Squares Problem hay trong Non-linear Optimization để phân tích ma trận Hessian,…
Trước hết chúng ta cùng xem lại một số khái niệm cơ bản.

I. Các khái niệm cơ bản

1. Ma trận chuyển vị và ma trận Hermitian

Cho $A \in \mathbb{R}^{m \times n}$ , ta nói $B \in \mathbb{R}^{n \times m}$ là chuyển vị của nếu $b_{ij}= a_{ji}, \forall 1 \le i \le n, 1 \le j \le m$ .
Nếu $A \in \mathbb{R}^{m \times n}$ thì $A^T \in \mathbb{R}^{n \times m}$ . Nếu , ta nói là một ma trận đối xứng (symmetric matrix).
Cho $A \in \mathbb{R}^{m \times n}$ , ta nói $B \in \mathbb{R}^{n \times m}$ là chuyển vị liên hợp của nếu $b_{ij}= \overline{a_{ji}}, \forall 1 \le i \le n, 1 \le j \le m$ , trong đó $\overline{a}$ là liên hợp phức của . Nếu chuyển vị liên hợp của một ma trận phức $A, A\in \mathbb{C}^{m \times n}$ bằng với chính nó, tức là , thì ta nói ma trận đó là Hermitian.

2. Ma trận xác định dương

Một ma trận vuông , $A \in \mathbb{R}^{n \times n}$ được gọi là xác định dương (positive definite) nếu ma trận đối xứng () và thỏa mãn với mọi $x$ \ne 0, x \in \mathbb{R}^{n}$ . Nói cách khác $x^TAx \ge 0$ với mọi và khi và chỉ khi .
Một ma trận vuông , $A \in \mathbb{R}^{n \times n}$ được gọi là ma trận nửa xác định dương (positive semidefinite) nếu ma trận đó đối xứng và thỏa mãn $x^TAx \ge 0, \forall x \in \mathbb{R}^{n}$ .
Nhận xét: Mọi ma trận xác định dương cũng là ma trận nửa xác định dương nhưng điều ngược lại không đúng, bởi vì ma trận xác định dương có ràng buộc khi và chỉ khi .
Với ma trận vuông $A \in \mathbb{R}^{n \times n}$ , ta có $x^TAx= \displaystyle \sum_{i=1}^{n} \sum_{j=1}^{n}A_{ij}x_ix_j$ , với đối xứng, ta có thể viết $x^TAx= \displaystyle \sum_{i=1}^{n}A_{ii}x_i^2+ 2 \displaystyle \sum_{i=1}^{n} \sum_{j=1}^{i-1}A_{ij}x_ix_j$ .
Ví dụ: Với ma trận $A=\begin{bmatrix} 9 & 6 \\ 6& 5 \end{bmatrix}$ ta có $x^TAx= 9x_1^2+12x_1x_2+5x_2^2= (3x_1+2x_2)^2+ x_2^2 \ge 0, \forall x$ . Hơn nữa khi và chỉ khi . Do đó là ma trận xác định dương.
Dễ thấy các phần tử trên đường chéo chính của ma trận xác định dương là các số dương. Thật vậy với ma trận xác định dương , xét với là unit vector thứ , ta có $x^TAx= e_i^TAe_i= A_{ii}>0$ với .

3. Schur complement

Cho $A \in \mathbb{R}^{n \times n}$ là ma trận xác định dương, viết lại như sau:
$A=\begin{bmatrix} A_{11} & A_{2:n,1}^T \\ A_{2:n, 1}& A_{2:n, 2:n} \end{bmatrix}$ .
Ma trận $S=A_{2:n,2:n}-\dfrac{1}{A_{11}}A_{2:n,1}A_{2:n,1}^T$ gọi là Schur complement của $A_{11}$ .
Bây giờ ta chứng minh cũng là ma trận xác định dương. Lấy vector $v \ne 0$ . Đặt $x= \begin{bmatrix} -\dfrac{1}{A_{11}}A_{2:n,1}^Tv \\ v \end{bmatrix}$ . Ta có $x \ne 0$ và
$x^TAx=\begin{bmatrix} -\dfrac{1}{A_{11}}A_{2:n,1}^Tv & v\end{bmatrix}\begin{bmatrix} A_{11} & A_{2:n,1}^T \\ A_{2:n, 1}& A_{2:n, 2:n} \end{bmatrix}\begin{bmatrix} -\dfrac{1}{A_{11}}A_{2:n,1}^Tv \\ v \end{bmatrix} =$
$\begin{bmatrix} -\dfrac{1}{A_{11}}A_{2:n,1}^Tv & v\end{bmatrix} \begin{bmatrix} 0 \\Sv \end{bmatrix}= v^TSv$ .
Do là ma trận xác định dương nên do đó , vậy cũng là ma trận xác định dương.

4. Gram matrix

Ma trận Gram là ma trận có dạng .
Ma trận Gram thì nửa xác định dương vì $x^T B^TBx = (Bx)^T(Bx) =||Bx||^2 \ge 0$ với mọi .
Ma trận Gram là xác định dương khi $||Bx||=0 \implies x=0$ hay các cột của là độc lập tuyến tính.

II. Cholesky Decomposition

1. Định nghĩa

Mọi ma trận xác định dương đều có thể được phân tích thành trong đó là ma trận tam giác trên (hoặc với là ma trận tam giác dưới) với các phần tử trên đường chéo chính là các số thực dương.
Ví dụ với ma trận xác định dương $3 \times 3$
$\begin{bmatrix} 25 & 15 & -5 \\ 15 & 18 & 0 \\ -5 & 0 & 11 \end{bmatrix}=\begin{bmatrix} 5 & 0 & 0 \\ 3 & 3 & 0 \\ -1 & 1 & 3 \end{bmatrix}\begin{bmatrix} 5 & 3 & -1 \\ 0 & 3 & 1 \\ 0 & 0 & 3 \end{bmatrix}$

2. Thuật toán tìm Cholesky Decomposition

Ta có thể viết lại như sau:
$A=\begin{bmatrix} A_{11} & A_{1, 2:n} \\ A_{2:n, 1}& A_{2:n, 2:n} \end{bmatrix}=\begin{bmatrix} R_{11} & 0 \\ R_{1, 2:n}^T& R_{2:n, 2:n}^T\end{bmatrix}\begin{bmatrix} R_{11} & R_{1, 2:n} \\ 0& R_{2:n, 2:n}\end{bmatrix}=$
$\begin{bmatrix} R_{11}^2 & R_{11}R_{1, 2:n} \\ R_{11}R_{1, 2:n}^T & R_{1, 2:n}^T R_{1, 2:n} + R_{2:n, 2:n}^TR_{2:n, 2:n} \end{bmatrix}$ .
Từ đây ta suy $R_{11}=\sqrt{A_{11}}$ , $R_{1,2:n}= \dfrac{1}{R_{11}}A_{1,2:n}$ ,
$R_{2:n,2:n}^TR_{2:n,2:n}=A_{2:n, 2:n}-R_{1, 2:n}^T R_{1, 2:n}$ .
Do đó $R_{2:n,2:n}^TR_{2:n,2:n}$ là phân tích Cholesky của $A_{2:n, 2:n}-R_{1, 2:n}^T R_{1, 2:n}= A_{2:n, 2:n}-\dfrac{1}{A_{11}}A_{2:n,1}A_{2:n,1}^T$ .
Để ý thấy biểu thức cuối là Schur complement của $A_{11}$ . Theo chứng minh ở phần I.3 thì đây là ma trận xác định dương kích thước $(n-1) \times (n-1)$ . Cứ tiếp tục truy hồi đến phân tích Cholesky $1 \times 1$ ta được kết quả. Ví dụ: Tìm phân tích Cholesky của ma trận
$\begin{bmatrix} 25 & 15 & -5 \\ 15 & 18 & 0 \\ -5 & 0 & 11 \end{bmatrix}$

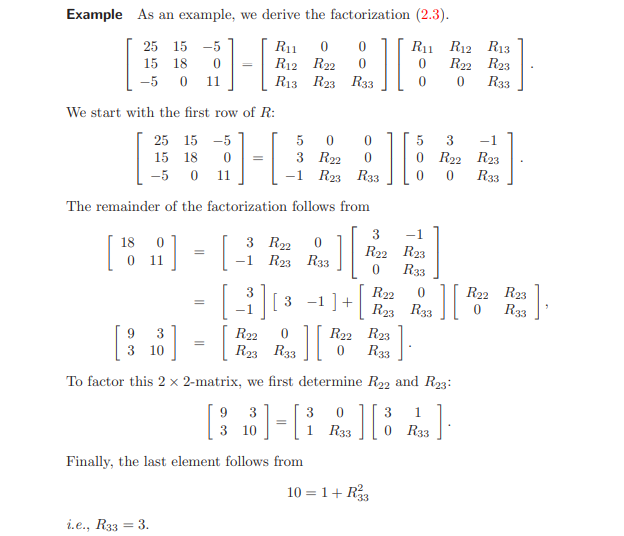
Để lập trình được, các phần tử trong ma trận được viết lại thành

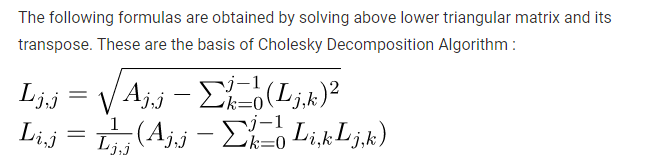
Code Python

import numpy as np
def CholeskyDecomposition(A):
  n=A.shape[0]
  L=np.zeros((n,n))
  for i in range(n):
      for j in range(i+1):
          if(i==j):
              temp=A[i,i]-np.sum(L[i,:i]*L[i,:i])
              if temp<0.0:
                  return 0.0
              L[i][i]=np.sqrt(temp)
          else:
              L[i][j]=(A[i][j]-np.sum(L[i,:j]*L[j,:j]))/(L[j][j])
  return L.T

Kết quả chạy

A=np.array([[25,15,-5],[15,18,0],[-5,0,11]])
R=CholeskyDecomposition(A)
print("R=",R)
print("Check")
print("A= ", R.T @ R)

R= [[ 5.  3. -1.]
 [ 0.  3.  1.]
 [ 0.  0.  3.]]
Check
A=  [[25. 15. -5.]
 [15. 18.  0.]
 [-5.  0. 11.]]

Kết quả cho ra đúng với kết quả ta làm ở trên.

Ta có thể dùng hàm cholesky trong thư viện .

Code Python:

R=np.linalg.cholesky(A)
print(L)
R_T=L.transpose()
print(R.dot(R_T))

Kết quả hoàn toàn giống.

III. Ứng dụng Cholesky Decomposition

1. Giải hệ phương trình tuyến tính

Giả sử hệ phương trình tuyến tính được biểu diễn dưới dạng ma trận Ax=b trong đó $A \in \mathbb{R}^{n \times n}$ là ma trận xác định dương, $x \in \mathbb{R}^{n}, b\in \mathbb{R}^{n}$ .
Ax=b
RR^Tx=b
$R^Tx= R^{-1}b$
$x=(R^T)^{-1}(R^{-1}b)$

Code Python

def CholeskyLinearEquation(A,b):
  #Find x with Ax=b
  L=np.linalg.cholesky(A)
  y=(np.linalg.inv(L)).dot(b)
  x=(np.linalg.inv(np.transpose(L))).dot(y)
  return x

A=np.array([[4,12,-16],[12,37,-43],[-16,-43,98]])
b=np.array([ -68 ,-191 , 364])
x=CholeskyLinearEquation(A,b)
print("x=",x)

Kết quả chạy: Hệ có nghiệm

x= [ 1. -2.  3.]

2. Least Squares Problem trong Linear Regression

Tham khảo bài viết tại https://alexisalulema.com/2018/01/20/cholesky-decomposition-for-linear-regression-with-tensorflow/

IV. Cholesky Decomposition của ma trận Gram

Cho ma trận có các cột độc lập tuyến tính.
Khi đó ma trận Gram là ma trận xác định dương. Có 2 cách để tính Cholesky Decomposition của .
1. Tính trực tiếp theo phương pháp ở trên.
2. Tính QR Decomposition của , tức là , khi đó , cũng là ma trận trong cách tính .
  Về phân tích QR mình sẽ trình bày ở bài sau.

V. Tài liệu tham khảo

http://www.seas.ucla.edu/~vandenbe/133A/133A-notes.pdf
https://alexisalulema.com/2018/01/20/cholesky-decomposition-for-linear-regression-with-tensorflow/
Ebook Machine Learning cơ bản, Vũ Hữu Tiệp.
https://www.geeksforgeeks.org/cholesky-decomposition-matrix-decomposition/
http://www.seas.ucla.edu/~vandenbe/133A/lectures/chol.pdf