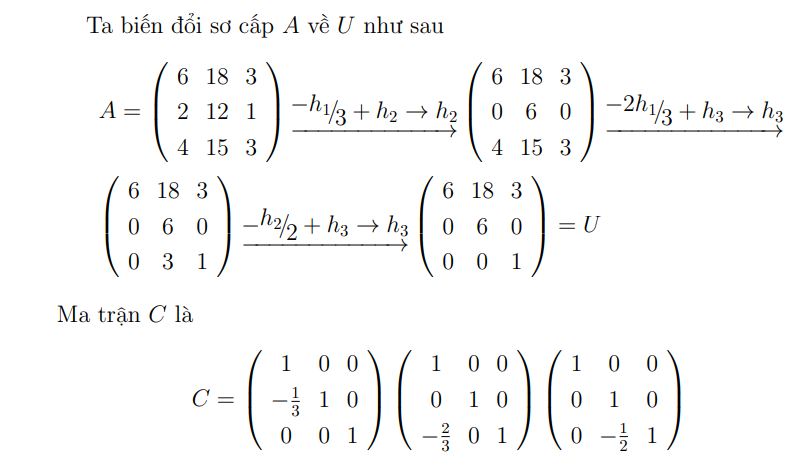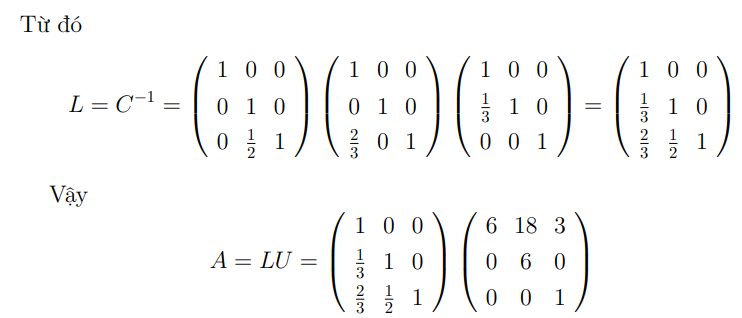I. Giới thiệu

Trong Machine Learning, chúng ta thường xử lý dữ liệu được biểu diễn dưới dạng ma trận, thường các ma trận này có kích thước lớn. Rất nhiều các bài toán học máy được giải quyết bằng cách sử dụng các phương pháp của Đại số tuyến tính. Trong các bài này mình sẽ trình bày về các phương pháp phân tích ma trận (hay Phân rã ma trận) (Matrix Decomposition).
Việc phân tích một ma trận là đưa ma trận đó về tích của 2 hay nhiều ma trận đặc biệt khác, thường là ma trận đường chéo và ma trận tam giác. Việc phân tích này nhằm mục đích dễ dàng tính định thức, tìm ma trận nghịch đảo, giải hệ phương trình tuyến tính, giảm chiều dữ liệu,… Matrix Decomposition cũng được ứng dụng trong bài toán về Hệ thống khuyến nghị (Recommendation System).
Một số phương pháp phân tích ma trận phổ biến như LU, QR, Cholesky, Eigen Decomposition (Chéo hóa ma trận), SVD,… Trong đó, SVD được sử dụng nhiều trong các thuật toán Học máy và Thị giác máy tính. Trong phần này mình sẽ trình bày một phương pháp đơn giản nhất là phân tích LU. (LU là viết tắt của Lower Triangular Matrix và Upper Triangular Matrix).

II. LU Decomposition

1. Định nghĩa

Cho $A \in \mathbb{R}^{n \times n}$ là một ma trận vuông, phân tích LU của là cách viết thành tích của 2 ma trận có dạng trong đó là các ma trận tam giác dưới và tam giác trên có cùng kích thước với . Người ta chứng minh được rằng mọi ma trận cấp thỏa mãn phân tích khi và chỉ khi các định thức con chính khác , phân tích sẽ duy nhất nếu thêm điều kiện các phần tử trên đường chéo chính của ma trận (hoặc ) đều bằng .
Ví dụ với ma trận vuông $3 \times 3$
$A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 1 \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & a_{33} \end{bmatrix}$
Vể mặt toán học, tìm phân tích này ta làm như sau:
Bước 1: Biến đổi sơ cấp ma trận thành ma trận tam giác trên . Bản chất của quá trình này là nhân với dãy ma trận không suy biến dạng tam giác dưới, giả sử dãy đó là , ta có
Bước 2: Do nên tìm được bằng công thức
$L=C_k^{-1}C_{k-1}^{-1}...C_1^{-1}=C^{-1}$
Ví dụ: Phân tích ma trận

$A=\begin{bmatrix} 6 & 18 & 3 \\ 2 & 12 & 1 \\ 4 & 15 & 3 \end{bmatrix}$

2. Thuật toán tìm LU Decomposition

Ta có thể biểu diễn như sau:
$\begin{bmatrix} A_{11} & A_{1, 2:n} \\A_{2:n,1} & A_{2:n,2:n}\end{bmatrix}= \begin{bmatrix} 1 & 0 \\L_{2:n,1} & L_{2:n,2:n}\end{bmatrix}\begin{bmatrix} U_{11} & U_{1, 2:n} \\0 & U_{2:n,2:n}\end{bmatrix}$
(Kí hiệu $A_{x_1:x_2, y_1:y_2}$ biểu diễn ma trận con lấy từ ma trận với hàng từ đến và các cột từ đến )
Suy ra $\begin{bmatrix} A_{11} & A_{1, 2:n} \\A_{2:n,1} & A_{2:n,2:n}\end{bmatrix} = \begin{bmatrix} U_{11} & U_{1, 2:n} \\U_{11}L_{2:n,1} & L_{2:n,1}U_{1,2:n} + L_{2:n, 2:n}U_{2:n, 2:n}\end{bmatrix}$
Từ đây ta có
$U_{11}=A_{11}, U_{1,2:n}=A_{1,2:n}, L_{2:n,1}=\dfrac{1}{A_{11}}A_{2:n,1}$
$L_{2:n,2:n}U_{2:n, 2:n}=A_{2:n, 2:n}-L_{2:n,1}U_{1,2:n}= \dfrac{1}{A_{11}}A_{2:n,1}A_{1,2:n}$
Đặt $S_{22}=\dfrac{1}{A_{11}}A_{2:n,1}A_{1,2:n} \in \mathbb{R}^{(n-1) \times (n-1)}$ ta có
$S_{22}=L_{2:n,2:n}U_{2:n, 2:n}$ là phân tích của $S_{22}$ . ( $S_{22}$ được gọi là Schur complement)
Thuật toán tìm phân tích được mô tả bởi:
Ví dụ: Tìm phân tích của

$A=\begin{bmatrix} 8 & 2 & 9 \\ 4& 9 & 4 \\ 6 & 7 & 9 \end{bmatrix}$

Ta có $A=\begin{bmatrix} 8 & 2 & 9 \\ 4& 9 & 4 \\ 6 & 7 & 9 \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 \\ L_{21} & 1 & 0 \\ L_{31} & L_{32} & 1 \end{bmatrix} \begin{bmatrix} U_{11} & U_{12} & U_{13} \\ 0 & U_{22} & U_{23} \\ 0 & 0 & U_{33} \end{bmatrix}$

Áp dụng các công thức ở trên ta được
Thuật toán ở trên có thể thể hiện mã giả (peusedocode) như sau

Code Python

import numpy as np
def LU_Decomposition(A):
  n=A.shape[0]
  U=A.copy()
  L=np.zeros((n,n))
  for i in range(n):
    L[i,i]=1
  for k in range(n-1):
    for j in range(k+1, n):
      L[j,k]=U[j,k]/U[k,k]
      U[j, k:n]=U[j,k:n]-L[j,k]*U[k, k:n]
  return L,U

Kết quả chạy thử:

A=np.array([[8.,2.,9.],[4.,9.,4.],[6.,7.,9.]])
print(A)
L,U=LU_Decomposition(A)
print("L=",L)
print("U=",U)

L= [[1.     0.     0.    ]
 [0.5    1.     0.    ]
 [0.75   0.6875 1.    ]]
U= [[ 8.       2.       9.     ]
 [ 0.       8.      -0.5    ]
 [ 0.       0.       2.59375]]

Kết quả cho ra đúng với ta làm ở trên.

Một cài đặt khác của thuật toán trên

import numpy as np
def LU_Decomposition(A):
  n= A.shape[0]
  L=np.zeros((n,n))
  U=np.zeros((n,n))
  M=A.copy()
  for i in range(n):
    U[i,i:]=M[i,i:]
    L[i:,i]=M[i:,i]/U[i,i]
    M[i+1:, i+1:]-=np.outer(L[i+1:,i], U[i, i+1:])
  return L,U

Kết quả cho ra hoàn toàn tương tự.

III. LU Decomposition with pivoting

Tổng quát hơn với ma trận vuông khả nghịch ta có phân tích , đó là phân tích có dạng trong đó là các ma trận tam giác như trên, là ma trận nhận được trong biến đổi sơ cấp hàng, hay được gọi là ma trận hoán vị (permutation matrix).
Ma trận chỉ có các phần tử . Ví dụ với ma trận $3 \times 3$
$A=\begin{bmatrix} 0 & 5 & 5 \\ 2 & 9 & 0 \\ 6 & 8 & 8 \end{bmatrix}=\begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ \dfrac{1}{3} & 1 & 0 \\ 0 & \dfrac{15}{19} & 1 \end{bmatrix}\begin{bmatrix} 6 & 8 & 8 \\ 0 & \dfrac{19}{3} & \dfrac{-8}{3}\\ 0 & 0 & \dfrac{135}{19} \end{bmatrix}$
Ta có thể sử dụng hàm trong thư viện

import numpy as np
from scipy.linalg import lu

A=np.array([[0,5,5],[2,3,0],[6,9,8]])
P,L,U=lu(A)
print("P=",P.T) #Trong hàm lu cho kết quả của A=PLU
print("L=", L)
print("U=", U)
print(P.T @ A)
print(L @ U)

Kết quả chạy

P= [[0. 0. 1.]
 [1. 0. 0.]
 [0. 1. 0.]]
L= [[1.         0.         0.        ]
 [0.         1.         0.        ]
 [0.33333333 0.         1.        ]]
U= [[ 6.          9.          8.        ]
 [ 0.          5.          5.        ]
 [ 0.          0.         -2.66666667]]
[[6. 9. 8.]
 [0. 5. 5.]
 [2. 3. 0.]]
[[6. 9. 8.]
 [0. 5. 5.]
 [2. 3. 0.]]

III. Ứng dụng LU Decomposition

1. Giải hệ phương trình tuyến tính

Cho hệ phương phương trình tuyến tính biểu diễn dưới dạng ma trận Ax=b trong đó $A \in \mathbb{R}^{n \times n}, x \in \mathbb{R}^{n}, b \in \mathbb{R}^{n}$ .

Ax=b

LUx=b

$Ux=L^{-1}b$

$x=U^{-1}(L^{-1}b)$

Cài đặt bằng Python, sử dụng hàm LU_Decomposition() đã viết ở trên.

def solve_system_equation(A,b):
  L,U=LU_Decomposition(A)
  x=np.linalg.inv(U).dot((np.linalg.inv(L).dot(b)))
  return x

A=np.array([[3,2,-1],[2,-2,4],[-1, 0.5, -1]], dtype=np.float32)
b=np.array([1,-2,0])
x=solve_system_equation(A,b)
print("x=",x)

Kết quả chạy
Hệ có nghiệm

x= [ 1.00000057 -2.00000129 -2.00000103]

2. Tính định thức

Với ma trận vuông khả nghịch ta có det(A)=det(LU)=det(L).det(U)

Mà L, U là các ma trận tam giác nên định thức bằng tích các phần tử trên đường chéo chính và đường chéo chính của đều là số nên det(L)=1
Do đó det(A)=det(U)

Ví dụ với ma trận $A=\begin{bmatrix} 8 & 2 & 9 \\ 4& 9 & 4 \\ 6 & 7 & 9 \end{bmatrix}$ , như đã làm ở trên thì có phân tích là
$A=\begin{bmatrix} 1 & 0 & 0 \\ \dfrac{1}{2}& 1 & 0 \\ \dfrac{3}{4} & \dfrac{11}{16} & 1 \end{bmatrix} \begin{bmatrix} 8 & 2 & 9 \\ 0 & 8 & \dfrac{-1}{2} \\ 0 & 0 & \dfrac{83}{32} \end{bmatrix}$
Khi đó $det(A)=\begin{vmatrix} 8 & 2 & 9 \\ 0 & 8 & \dfrac{-1}{2} \\ 0 & 0 & \dfrac{83}{32} \end{vmatrix}= 8.8.\dfrac{83}{32}=166$

Kiểm tra lại bằng Python

def determinant_of_matrix(A):
  L,U=LU_Decomposition(A)
  det=np.linalg.det(U)
  print("U=",U)
  return det

A=np.array([[8.,2.,9.],[4.,9.,4.],[6.,7.,9.]])
print("Det by library: ",np.linalg.det(A))
print("Det by LU Decomposition: ",determinant_of_matrix(A))